
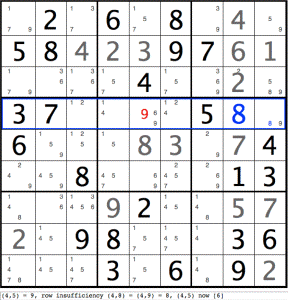
Row 4 is highlighted with a blue rectangle, indicating the program has reported a row insufficiency on the line below the board, repeated here:
(4,5)=9, row insufficiency (4,8) = (4,9) = 8, (4,5) now [6]

Graphically, the highlighted numbers in row 4 indicate that a contradiction results if (4,5)=9. If, as highlighted, (4,5)=9, (4,9) (the last cell) must be 8 (since 9 has now been taken). But (4,8) is already set to 8. Therefore (4,5) can never be 9. The red value 9 can be cancelled from (4,5), leaving just 6.
Again, row 4 is highlighted using a blue rectangle to indicate a row insufficiency.
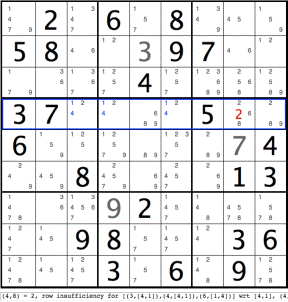
(4,8)=2, row insufficiency for [(3,[4,1]),(4,[4,1]),(6,[1,4])] wrt [4,1], (4,8) now [6,8]

Graphically, the highlighted numbers in row 4 indicate that a contradiction results if the 2nd last cell (4,8)=2. If (4,8)=2, three cells, namely cells 3, 4 and 6, in the row must share two values, namely 1 and 4 (since 2 has now been taken). Since three cells cannot split two values, we have a contradiction. Therefore (4,8) can never be 2. The red value 2 can be removed from (4,8), leaving [6,8].
Column 5 has been highlighted using a blue rectangle to indicate column insufficiency.
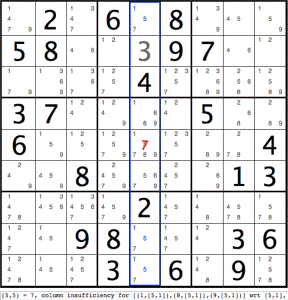
Zooming in, we have:
(5,5)=7, column insufficiency for [(1,[5,1]),(8,[5,1]),(9,[5,1])] wrt [5,1], (5,5) now [1,5,8,9]
|

|
Graphically, the highlighted numbers in column 5 indicate that a
contradiction results if the middle cell (5,5) takes on value 7.
If (5,5)=7, three cells in the column, namely cells 1, 8 and 9, must share two values, namely 1 and 5 (since 7 has now been taken). Again, since three cells cannot split two values, we have a contradiction. Therefore (5,5) can never be 7. The red value 7 can be removed from (4,8), leaving [1,5,8,9] (the 5 here is partially obscured by the displayed red 7). |
The 3x3 area beginning at cell (1,7) has been highlighted using a blue square to indicate 3x3 area insufficiency.
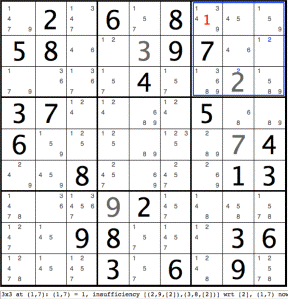
Considering now just the area delimited by cells (1,7) and (3,9):
3x3 at (1,7): (1,7)=1, insufficiency [(2,9,[2]),(3,8,[2])] wrt [2], (1,7) now [3,4,9]
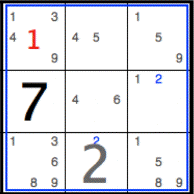
Graphically, the highlighted numbers in the square indicate that a contradiction results if the top-left cell (1,7) is set to 1. If (1,7)=1, two cells, namely the middle one of the bottom row (3,8) and the rightmost one on the middle row (2,9), must share the value 2 (since 1 is no longer available). Since two cells cannot split a single value, we have a contradiction. Therefore (1,7) can never be 1. The red value 1 can be deleted from (1,7), leaving [3,4,9].