Sudoku Sandiway

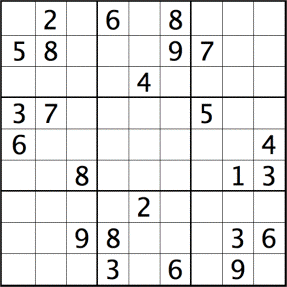
The game sudoku is a logic puzzle. The idea of the puzzle is to take a partially-filled 9 x 9 square, such as the one shown above, and fill in the missing cells such that numbers 1 through 9 are assigned uniquely for:

• each row,
• each column,
• and each of the 9 3 x 3 squares

(Here, we will adopt the convention that the initial values supplied are in black, and the values to be assigned by the puzzle solver are shown in gray, respectively.)

The goal for the puzzle solver is to not to simply fill in the missing numbers but to find a logically-justifiable way of determining the missing numbers without resorting to guessing their values. In other words, the puzzle should be solved using logic methods.

This program (written as an illustration of logical reasoning) shows you how to solve these puzzles in a step-by-step manner, justifying each number assignment with respect to the three constraints.

[By the way, the program was written using Sicstus Prolog for the logic engine and the TCK/TK toolkit for the user interface elements.]

We can determine the possible values for each cell in the initial puzzle as shown below:

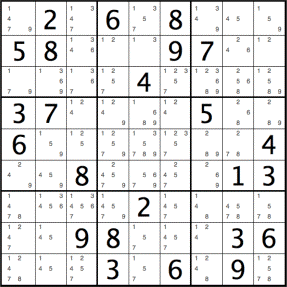
We will use the convention of numbering the cells from left to right and top to bottom with respect to row and column positions (row,column) starting with position 1.

For example, in the above diagram, the top-left corner, namely cell (1,1), has 4 possible values [1,4,7,9], as shown using the little numbers, repeated below.

Adjacent cells (1,2), (2,1) and (2,2) have supplied (unique) values 2, 5 and 8, respectively.

The missing possibilities for cell (1,1), namely [2,3,5,6,8], are excluded by the row, column and 3 x 3 square uniqueness constraints: i.e. they are already taken up somewhere else either in column 1 ([5,3,6]), row 1 ([2,6,8]) or the 3 x 3 sub-square delimited by cells (1,1) through (3,3) ([2,5,8]).

This program will winnow the available choices for cell (1,1) down to just 1 through reasoning by contradiction using one of a few heuristics. The program will display its steps in the reasoning process using both text messages and graphical illustration. Examples are given below of each type of heuristic.

Click on the various sections below for further information:

• Board setup.
• Running a puzzle

Heuristics:

• Heuristic 1a: Simple row, column or 3 x 3 area inconsistency. (Only red highlighting is used.)
• Heuristic 1b: Row, column or 3 x 3 area insufficiency. (Blue and red highlighting is used.)
• Heuristic 2: Row, column or 3 x 3 area set cover elimination. (Green and red highlighting is used.)
• Heuristic 3: Unique row/column combination. (Gold highlighting is used.)
• Heuristic 4: Unique mention in row, column or 3 x 3 area. (Brown and red highlighting is used.)
• Heuristic 1+: Boosted version of the inconsistency/insufficiency checker factoring in the two uniqueness heuristics. (Multiple highlighting is used.)

• Example puzzles and their solutions supplied with the program.
• The "Unsolvable 11" from SudokuList. Solutions.

Suggestions and comments to sandiway at email dot arizona dot edu.