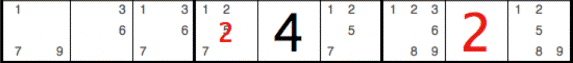
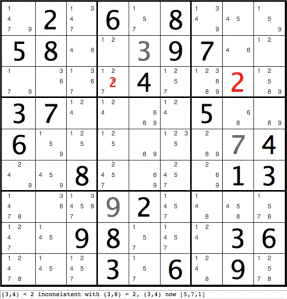
Two cells in row 3 have been highlighted in red indicating that the program has reported a row inconsistency on the line below the board, repeated here:
(3,4)=2 inconsistent with (3,8) = 2, (3,4) now [5,7,1]
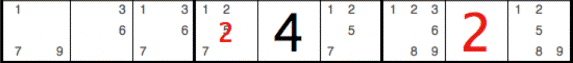
Graphically, the highlighted numbers in row 3 indicate that a contradiction results if (3,4)=2. If (3,4)=2, this is inconsistent with the prior value of 2 for (3,8). Hence, we have a contradiction. And (3,4) cannot have possibility 2. The red value 2 can be removed from cell (3,4), leaving values [5,7,1] (5 is partially obscured here by the highlighted 2.)
Two cells in column 4 has been highlighted in red to indicate column inconsistency.
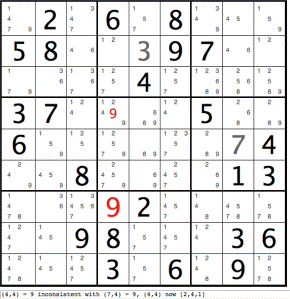
Zooming in, we have:
(4,4)=9 inconsistent with (7,4)=9, (4,4) now [2,4,1]
|

|
Graphically, the highlighted numbers in column 4 indicate that a
contradiction results if the cell (4,4) takes on value 9.
If (4,4)=9, this is inconsistent with the previously determined value for cell (7,4). Since two cells cannot contain the same value in a single column, we have a contradiction. Therefore (4,4) can never be 9. The red value 9 can be removed from (4,4), leaving remaining possibilities [1,2,4]. |
The 3x3 area beginning at cell (7,7) has been highlighted using a red square to indicate 3x3 area inconsistency.
Considering now just the area delimited by cells (7,7) and (9,9):
3x3 at (7,7): (8,7)=2 inconsistent with (9,9)=2, (8,7) now [1,4]
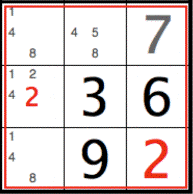
Graphically, the highlighted numbers in the square indicate that a contradiction results if the left cell in the middle row (8,7) is set to 2. (8,7)=2 is inconsistent with the previously determined value 2 for cell (9,9). Since we cannot have two cells with the same number in the same 3 x 3 area, we have a contradiction. Therefore (8,7) cannot be 2. The red value 1 can be deleted from (8,7), leaving [1,4].