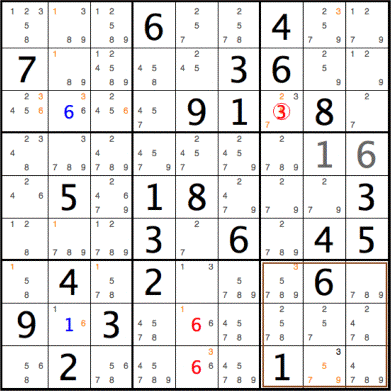
Establishing (8,5)=6
- (8,5) must be 6 (shown in red) if it cannot
be 1.
[6,1] are the only two possibilities at this stage for the cell.
(1 is highlighted in orange.)
- (8,5) cannot be 1 if the
cell on the same row, namely (8,2), must be 1.
(This pivotal value 1 is highlighted in blue).
- (8,2) must be 1 if the other possibility for
the cell, namely 6, cannot be true.
(6 for (8,2) is highlighted in orange.)
- (8,2) cannot be 6 if the cell on
the same column, namely (3,2), must be 6.
- (3,2) must be 6 (highlighted in blue) if it cannot be 3.
(3 for (3,2) is highlighted in orange.)
- But (3,2)
cannot be 3 based on the original assumption that (3,7), a cell on the
same row as (3,2), was 3 to begin with.
|
Establishing (9,5)=6
- (9,5) must be 6 (shown in red) if it cannot be
3.
[6,3] are the only two possibilities at this stage for the cell.
(3 is highlighted in orange.)
- (9,5) cannot be 3 if the
cell on the same row, namely (9,8), must be 3.
- (9,8) must be 3 due as indicated in the 2nd message.
[Note: the indentation indicated by the dots (ellipsis)
indicates it is a subpart of the larger proof.]
In the 3x3 area anchored at
(7,7) (highlighted in brown/orange), 3 is uniquely mentioned in cell (9,8).
In other words, it cannot take any of the values [5,7,9] because then
3 would be "lost", i.e. not assigned in the 3x3 area.
(The values [5,7,9] in (9,8)
eliminated by the uniqueness requirement (Heuristic 4) are highlighted
in orange.)
- 3 is uniquely mentioned in (9,8) with respect to the 3x3 area at
(7,7) if the only other mention in (7,7) can be eliminated.
(3 in (7,7) is highlighted in orange.)
- But (7,7) cannot be 3 based on the original assumption that (3,7),
a cell on the same column as (7,7), was 3 to begin with.
|