Row, Column and 3x3 Set Cover Elimination Messages Explained

There are three examples in this series.

It is not always necessary to find a direct contradiction between two single numbers. In some cases, it is possible to assume a subgroup of cells must share or cover a subset of values from 1 to 9, and therefore infer that other relevant cells cannot take on any of those values. This is a more powerful heuristic than the previous ones we have covered.

Example 1

We illustrate this principle with a row that involves a contradiction derived from 4 cells with respect to a set of 4 values.

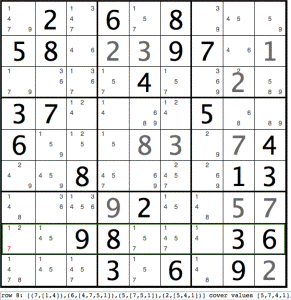
Below, row 8 is highlighted using a green rectangle to indicate a row set cover inconsistency.

row 8: [(7,[1,4]),(6,[4,7,5,1]),(5,[7,5,1]),(2,[5,4,1])] cover values [5,7,4,1], (8,1) must be truncated.

Graphically, the highlighted numbers in row 8 indicate that a contradiction results for cell (8,1) for values 1 and 7.

Note that 4 cells, namely 2,5,6 and 7 cover values [5,7,4,1] for row 8. In other words, whatever happens, these 4 cells must be assigned, i.e. cover, these 4 values among themselves. (It is not necessary to determine who gets what at this stage.)

If the 4 cells have taken [5,7,4,1], we have a contradiction since cell (8,1) contain values [1,7] (they have been assigned to the 4 cells). Therefore (8,1) can never be 1 or 7. The red values [1,7] can be removed from (8,1), leaving just 2.

Example 2

The next example for columns is slightly more complex than the previous one for rows. Again, we have 4 cells covering 4 values, but the contradiction this time affects two cells instead of just one.

Column 2 has been highlighted using a green rectangle to indicate a column cover inconsistency.

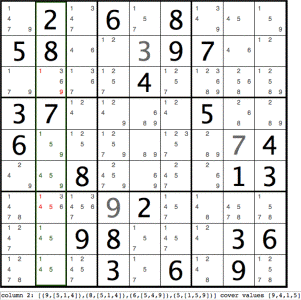
Zooming in, we have:

column 2: [(9,[5,1,4]),(8,[5,1,4]),(6,[5,4,9]),(5,[1,5,9])] cover values [9,4,1,5], [(2,[1,3,6,9]),(7,[1,3,4,5,6])) must be truncated. Graphically, the highlighted numbers in row 2 indicate that a contradiction results for cells 3 and 7 for values 1,4,5 and 5.
Note that 4 cells, namely 5,6,8 and 9 cover values [9,4,1,5] for column 2. (In fact, cells 8 and 9 are identical.)
Again, whatever happens, these 4 cells must be assigned, i.e. cover, these 4 values among themselves. (It is not necessary to determine which cell gets what value at this stage.)
If the 4 cells have taken [9,4,1,5], we have a contradiction since cells 3 and 7 contain values [1,9] and [1,4,5], respectively (and these values have been allocated to the 4 cells mentioned earlier).
Therefore cells 3 and 7 can never be [1,9] or [1,4,5], respectively. And we can remove these red values, leaving [3,6] for both cells 3 and 7.

Example 3

The last example illustrates the same rule in the case of a 3x3 area. It is a bit simpler than the previous two cases. This example involves just 3 cells covering 3 values causing a contradiction for one other cell.

The 3x3 area beginning at cell (7,7) has been highlighted using a green square to indicate a 3x3 area cover inconsistency.

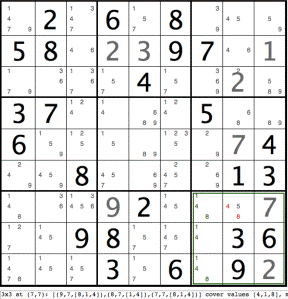
Considering now just the area delimited by cells (7,7) and (9,9):

3x3 at (7,7): [(9,7,[8,1,4]),(8,7,[1,4]),(7,7,[8,1,4])] cover values [4,1,8], must truncate (7,8,[4,5,8]).

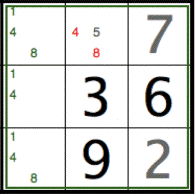
Graphically, the highlighted numbers in the square indicate that a contradiction results for cell (7,8) for values 4 and 8.

Note that the 3 cells on the left side, namely (7,7), (8,7) and (9,7), cover the 3 values [4,1,8] for this 3x3 square.

Again, whatever happens, these 3 cells must be assigned, i.e. cover, these 3 values among themselves. (It is not necessary to determine which cell gets what value at this stage.)

If the 3 cells have taken [4,1,8], we have a contradiction since cell (7,8) contain values [4,5,8], and 4 and 8 have been allocated to the 3 cells mentioned earlier.

Therefore cell (7,8) can never be 4 or 8. We can remove these red values, leaving just value 5.