a natural number, e.g. 1 in run/1, refers to the number of arguments required for a predicate or functor, e.g. the predicate run with one argument.
atoms are the simplest form of Prolog terms. They have no internal structure. Atoms come in two varieties, quoted and unquoted. Quoted atoms are delimited by single quotes, e.g. 'v*' or 'Tpast', and can contain characters from any script, e.g. '花子'. Unquoted atoms must begin with a lowercase letter, and thereafter can contain mixed case letters and digits and underscore, but no punctuation characters. (Tokens that begin with an uppercase letter (or underscore) are variables, not atoms, e.g. Mary.)
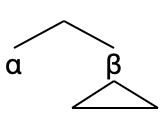
c-command is the third simplest
relation available between syntactic objects. Sisterhood, e.g. X and
Y are sisters in {X, Y}, is the simplest. Term of is the next
simplest, encoding dominance. Then c-command is sisterhood + term
of. Example: α c-commands β and all terms of β. Ideally, term would
be limited to the local search domain, i.e. Phase.
See also Phase, sister and term.
conceptual-intentional interface. Narrow syntax output syntactic objects (SOs) that will be interpreted by syntactico-semantic processing at the C-I (or CI) interface. The Minimalist Machine converges if it generates a single SO from an initial list of heads.
Prolog terms are either simple, i.e. an atom, or are compounds, consisting of a functor name plus internal structure in the form of arguments. An example of a compound term is a(a(a), b(b,b)) with functor name a and arity 2. In this case, both arguments of a/2, i.e. a(a) and b(b,b) themselves are also compound terms.
a machine configuration consists of the list of heads (ordered as a queue), the current syntactic object (SO) and a stack (of theta-relevant SOs). The current SO and the list of heads can be considered as the current Workspace. The stack is not conceptually necessary, but it is maintained for computational efficiency.
a derivation converges if it begins with a list of heads drawn from LEX and iterated Merge produces a single syntactic object (SO) with no unchecked uninterpretable features.
In the Minimalist Machine, we still announce a parse even when there are uninterpretable features remaining. This is for convenience, e.g. in the case of parsing relatives clauses DPs such as the man who(m) I know, the DP has an unvalued uninterpretable Case feature.
Kayne's Doubling Constituent (DC) theory of pronominal coreference posits a pronominal/R-expr pair (to be read at the C-I interface as being coreferential). For example, the pair he-John initially forms a DC {d, {he, {d, John}}}, in which we have two DPs. In Johni thinks hei is smart, the pair he-John initially Merges as the argument of smart, but only he gets a theta role. Subsequently, the junior partner in the DC, i.e. John must raise to its own theta position.
in the probe-goal system, economy arises when more than one feature can be valued during a single probe-goal interaction. Two separate probe-goal interactions to achieve multiple feature valuation will be blocked by multiple feature evaluation by a single probe-goal when available. This is used in the Pesetky & Torrego story about T to C movement.
edge is a feature of a head signaling whether a 2nd Merge is permitted while projecting the head. In (a) below, Head projects and labels both sets as LBL. The lower label on {Head, β} is given by the rule Head + non-head β -> Head labels. The upper label on {α, {Head, β}} is given by feature edge on Head. In some theories, e.g. POP, prominent feature matching, <ɸ,ɸ>, is used to license the structure {XP, YP}, assuming XP (or YP) do not move.
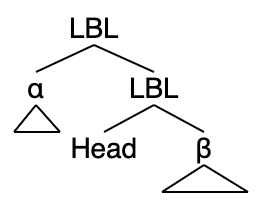 (a) |
In the Minimalist Machine, this edge feature is used in the case of some v's to permit leftwards TH/EX (Sobin), as in there were several prizes awarded, cf. ??there were awarded several prizes, for interrogative C to host a Wh-fronted DP, for T to permit a surface subject, and for the relative complementizer to host a wh-relative DP in its left edge, as in the man whom I knew prior to further raising of head man outside the relative clause to form a new DP in conjunction with the.
simplest Merge applies
only to the root of the current syntactic object (SO) being
constructed. No tuck-in, or Merge into a term of a complex SO, is
permitted.
Thus, cyclicity is observed.
Given two different Workspace (WS) objects, X and Y, simplest External Merge forms a new WS containing {X, Y}, but not X and Y. Other WS objects not participating in External Merge are also in the new WS. That is all.
Note: External Merge obeys the No-Tampering Condition (NTC), a natural requirement for computational efficiency, i.e. External Merge leaves both X and Y unchanged.
External Merge is computationally less efficient than Internal Merge. Why does I-Language have External Merge then? Answer: predicate-argument structure.
In the Minimalist Machine, the Heads queue and the current SO together comprises the Workspace. The External Merge operation takes H, the current front of the Heads queue, and the current syntactic object (SO), and computes the updated current SO {H, SO}. The Heads queue is also updated to be the rest of the queue.
If WS = ([H|Heads], SO), updated WS' = (Heads, {H, SO}).
See also Internal Merge, list, NTC and Workspace.
independently formed sub-Workspace syntactic objects (SOs) can be assembled into an n-ary set (n > 1) provided they meet parallelism requirements. Note, FormSet is not Merge.
Examples involving FormSet including stacked relatives such as the student who lives here who studies English and conjunction, as in the student who lives here and who studies English or John arrived and met Bill. (The Minimalist Machine currently partially implements FormSet.)
a Prolog term can either be an atom or a compound. Compounds will have a functor name and arity (> 0). For example, so/5 is a compound term, and is the internal representation of a syntactic object constructed by predicate mkSO/2.
Note, in SWI-Prolog, we have:
?- X = a, atom(X), functor(X,Name,Arity). X = Name, Name = a, Arity = 0.
a goal is an appropriate syntactic object (SO) with an (unvalued) uninterpretable feature. Currently, the only appropriate SOs are theta-relevant DPs.
For example, (theta-relevant) DPs have uninterpretable Case. Such DPs are sent to the stack when Merged, e.g. as the internal or external argument of a predicate. In the Minimalist Machine, rather than traverse the c-command domain looking for a matching goal, probes will inspect the stack to quickly find the nearest matching goal. For example, probe T with unvalued ɸ-features will find a DP on the stack with unvalued Case and interpretable ɸ. T values Nominative Case on the DP and the DP values T's ɸ-features. Similarly, v* with unvalued ɸ-features will find a DP on the stack. v* values Accusative Case on the DP and the DP values v*'s ɸ-features. This is the Chomsky Derivation by Phase story.
a head is the smallest syntactic object (SO) in the grammar, it contains no sub-structure. Heads may project upwards to complex phrases, i.e head phrases with internal structure. Projection is defined via Labeling rules.
Given a complex syntactic object (SO) X in the Workspace (WS), Internal Merge takes X and a term of X, call it Y, and forms a new WS containing {X, Y}, but not X. Other WS objects are also present in the new WS. That is all.
Note: Internal Merge obeys the No-Tampering Condition (NTC), a natural requirement for computational efficiency, i.e. Internal Merge leaves both X and Y unchanged.
Internal Merge is the computationally most efficient operation forming hierarchical structure, assuming term is more efficient than pick a distinct Y in WS.
In the Minimalist Machine, the Heads queue and the current SO together comprises the Workspace. The Internal Merge operation takes the current syntactic object (SO) and an accessible term of SO, call it X, and computes the updated current SO {X, SO}. The Heads queue is unchanged.
If WS = (Heads, SO), updated WS' = (Heads, {X, SO}), X an accessible term of SO. Accessibility is defined in terms of local Phase.
See also External Merge, Phase, term and Workspace.
a feature is interpretable is if it is meant to be read at the CI (or C-I) interface.
In the Minimalist Machine, interpretable features for heads are listed separately from the uninterpretable features in grammar.pl
the lexicon (LEX) lists possible heads and their features. Heads enter the Workspace from LEX as primitive syntactic objects.
In the Minimalist Machine, the input to the machine is a list of names of heads. First, the names are looked up in LEX and a list of heads is formed. This list is an ordered Workspace (WS). Merge applies to this WS (and independently, to sub-WSs). Convergence obtains when the WS reduces via Merge to a single syntactic object (SO).
Prolog lists are delimited by square brackets. Items, if they exist, typically are comma-separated, e.g. [1, 2, 3] or [] (the empty list).
Also, generally [X|L] denotes a list with first element X and L the remaining items in the list, e.g. in list [1, 2, 3], X would be 1 and L would be [2, 3].
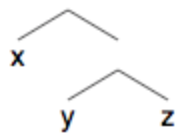
binary set Merge and pair Merge are defined over Workspace objects in the Minimalist Machine.
In
the browser interface, conventional binary branching tree structure
is shown for binary set Merge.
For example, in (a), y set
Merges with z. Then {y, z} set Merges with
x.
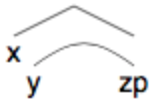
Notation: to differentiate set from pair Merge, we use an
arc to connect a SO to its adjunct SO.
In (b), the adjunct
y attaches to zp. The pair-merged structure then
merges with x.
 (a) |
 (b) |
grammatical heads each have a name, an atom or quoted atom, e.g. 'v*' or d. Names are used for input and output. Names are not syntactic objects. The system will construct syntactic objects, one per input name. In list [..,x,..,x,..], x a name, two (independent) repetitions of the syntactic head corresponding to name x will be built.
the No-Tampering Condition (NTC) means all syntactic operations, e.g. External and Internal Merge, must leave its participants intact, i.e. unchanged.
Note: the NTC subsumes the Extension Condition. Arguably, the NTC also subsumes Inclusiveness.
In the Minimalist Machine, occ is an internal bookkeeping feature used to keep track of occurrences of phrases. It is accessed at Spell-out to determine which occurrence should be pronounced.
At the time of implementation, such a violation of the Non-Tampering Condition (NTC) seems unavoidable. The occ feature is neither an uninterpretable nor an interpretable feature. One kludge is to view the occ feature as not belonging to Narrow Syntax. Another idea would be to compute the effect of occ from hierarchy at EXT, but this is not always possible, e.g. in the case of some Psych predicates.
The local search domain for Merge and probe-goal is a Phase. For Internal Merge, terms of the current syntactic object (SO) can only be accessed down to the edge of the phrase headed by a Phase head. In the current grammar, complementizers, possessive 's and -self are declared to be Phases.
Example: we take 's to be a Phase head given John's picture of himself/*him (coreferential with John), *John saw Mary's picture of himself, John saw a picture of himself.
In the Minimalist Machine, for efficient computation, search domains for theta-relevant phrases are defined via the stack. In addition to such phrases, the stack may contain a Phase boundary item, beyond which search cannot proceed deeper.
the name of a Prolog
predicate. The
a head with an (uninterpretable) unvalued feature is a probe. When such a head is Merged to a syntactic object (SO), it triggers a probe of its c-command domain, i.e. the current SO, for a matching goal. Examples include interrogative C, with uninterpretable wh, probing for a wh-DP, and T, with uninterpretable-ɸ, probing for a DP with ɸ-features.
In the Minimalist Machine, for search efficiency, probes have only a single opportunity to find a goal, viz. when it is Merged with the current SO. This happens when the probe head is at the front of the queue of the Workspace. We never (need to) search the SO for a probe.
In Prolog, a term is an atom
or a variable or a compound term. A compound term has a functor and
arity > 0.
Examples: 'Tpast' is an atom, X is a variable (as
it begins with an uppercase letter), and a(b, c) is a
compound term with arity 2 and sub-terms b and
c.
See also arity, atom and compound. See also (non-Prolog) term.
Referential expression, e.g. a name such as John. To be contrasted with anaphors, e.g. himself and pronominals, e.g. he. See also Doubling Constituent (DC).
in a complex syntactic object (SO) {X, Y}, SOs X and Y are sisters. Sister of is the simplest possible relation between two objects.
See also term and c-command.
a stack is a device used by the Minimalist Machine to facilitate efficient search of the c-command domain for theta-relevant DPs. Notice that when a head α is (initally) Merged with the syntactic object (SO) β computed so far, as in (a) below, β, down to the next Phase, is the c-command domain of the head.
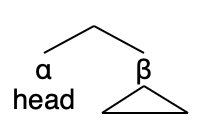 (a) |
During the construction of β, theta-relevant DPs are sent to the stack. Phase heads, when Merged, also mark the extent of the stack. Instead of searching β top-down, when α is a probe, the machine matches the top-of-stack (TOS) as a goal for α. In the ideal case, no further inspection, i.e. search (down the stack), is required.
a syntactic object is
either a head (drawn from LEX) or the result of Merge.
See also FormSet for extensions.
term is the second simplest relation available to I-language. A term of a syntactic object SO is any phrase properly dominated by SO. Term is a binary relation.
More formally, if X ∈ SO, X is a term of SO. X is also a term of Y if Z ∈ Y and X is a term of Z.
See also sister and c-command. Also Prolog term.
refers to the item on top of the current stack.
a feature is uninterpretable is if it is not meant to be read at the CI (or C-I) interface. These features are Narrow Syntax internal and should be valued (or checked) by appropriate c-commanding heads, called probes, prior to convergence.
In the Minimalist Machine, uninterpretable features for heads are listed separately from the interpretable features in grammar.pl
Merge is defined on a WS containing syntactic objects (SOs). The WS is initally populated by heads drawn from LEX.
In the Minimalist Machine, WS = (Heads, SO), in which Heads is the current list of heads and SO the current syntactic object. WS Heads is pre-ordered as a queue for fast computation. Machine actions are defined over possible current SOs and the head currently at the front of the Heads queue. For example, John saw Mary and Mary saw John are generated from different WS queues, the former from [mary, d, see, 'v*', [john, d], 'Tpast', c] and the latter from [john, d, see, 'v*', [mary, d], 'Tpast', c].
Sub-Workspaces may also be defined as sub-lists in the queue. For example, both queues above contain a sub-list, viz. [john, d] and [mary, d], respectively. A subject of a transitive clause is formed in its own sub-WS. Once a sub-WS is complete, i.e. a single SO has been formed (and no heads remain unused), the completed SO is inserted into the head queue of the higher WS. It will then be available for further Merge.
Example: consider the queue of heads [mary, d, see, 'v*', [john, d], 'Tpast', c] shown previously. Merge in the main WS proceeds until the sub-head list [john, d] is encountered. At this point, the current SO will be {v*, {see, {d, mary}}}. The machine next enters a new sub-WS and constructs the external argument {d, john}. It then pops up to the main WS with the queue now being [{d, john}, 'Tpast', c] and the SO {v*, {see, {d, mary}}} as before. In the next step, external Merge can then apply to the head of the queue and the current SO to produce {{d, john}, {v*, {see, {d, mary}}}}. After this operation, the remaining queue of heads will be ['Tpast', c].
Note: multiple sub-WSs are used as input to FormSet.
See also External Merge and Internal Merge.