8 Piece Calendar Puzzle

Goal: arrange the pieces to cover everything except the month and day for each day of the year.

There are multiple possible solutions, e.g. for the month of September.

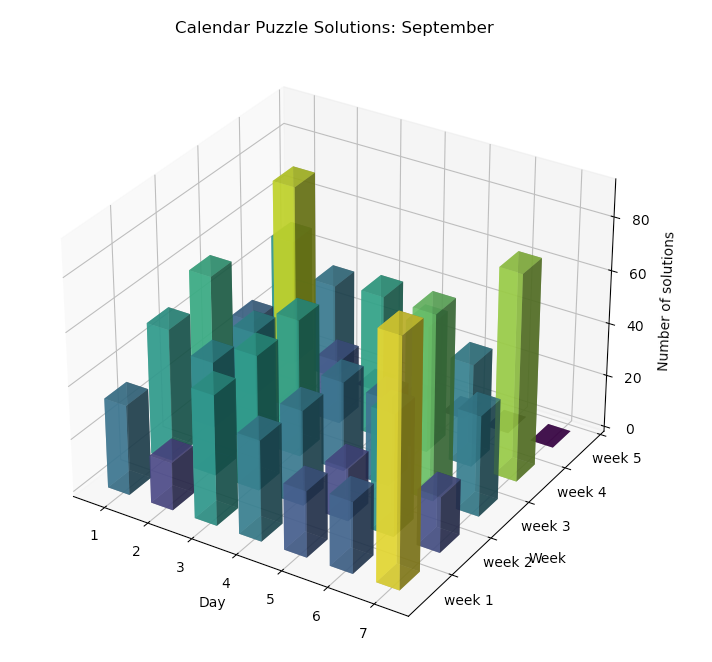
Simple search problem for fitting the 8 pieces.

Benchmarks

Apple M1 Max on MacBook Pro 16":

Model Name:		MacBook Pro
Model Identifier:	MacBookPro18,2
Model Number:		Z14V001H4J/A
Chip:			Apple M1 Max
Total Number of Cores:	10 (8 performance and 2 efficiency)
Memory:			64 GB

Single day parallel:

?- time(solveP(sep,7)). 
% 3,994 inferences, 0.007 CPU in 263.628 seconds (0% CPU, 558680 Lips) 
true. 
?- prBoards(N).

solveP(Mon,Day) :-
	pieces([P|_]),
	retractall(soln(_)),
	board(B),
	month(Mon,B),
	day(Day,B),
	findall(B,place1(P,B),L),
	copytermL(L,Lp),
	concurrent_maplist(solve_nf,Lp).

%% nf = no-fail
%% assume piece 1 has been placed
solve_nf(B) :-
	pieces([_|Ps]),
	placeL(Ps,B),
	assertz(soln(B)),
	fail.
solve_nf(_).

All soln/1 are listed by prBoards/1.

Month of September in parallel:

solve(Mon,Day,N) :-	% collect all N solutions
	pieces(Ps),
	board(B),
	month(Mon,B),
	day(Day,B),
	findall(B,placeL(Ps,B),Sols),
	length(Sols,N).

Program Explained

The Board

Setup:

%% 7 x 7 square with cells blocked off
%% Row 0. 1. 2. 3. 4. 5. 6. Col
%% 0.  months
%% 1.  months
%% 2.   1  2  3  4  5  6  7
%% 3.   8  9 10 11 12 13 14
%% 4.  15 16 17 18 19 20 21
%% 5.  22 23 24 25 26 27 28
%% 6.  29 30 31
board([[_,_,_,_,_,_,0],
       [_,_,_,_,_,_,0],
       [_,_,_,_,_,_,_],
       [_,_,_,_,_,_,_],
       [_,_,_,_,_,_,_],
       [_,_,_,_,_,_,_],
       [_,_,_,0,0,0,0]]).

%% board B given Row/Col finds cell Val
board(B,Row,Col,Val) :-	nth(Row,B,R), nth(Col,R,Val).

pieces([1,2,3,4,5,6,7,8]).	% 8 piece puzzle

Months and Days

Months on the board:

%% month(Name, Board)
month(jan,[[ja|_]|_]).
month(feb,[[_,fe|_]|_]).
month(mar,[[_,_,mr|_]|_]).
month(apr,[[_,_,_,ap|_]|_]).
month(may,[[_,_,_,_,my|_]|_]).
month(jun,[[_,_,_,_,_,jn|_]|_]).
month(jul,[_,[jl|_]|_]).
month(aug,[_,[_,au|_]|_]).
month(sep,[_,[_,_,se|_]|_]).
month(oct,[_,[_,_,_,oc|_]|_]).
month(nov,[_,[_,_,_,_,no|_]|_]).
month(dec,[_,[_,_,_,_,_,de|_]|_]).

Day on the board:

%% day(Nth, Board)
day(N,B) :-
	Row is floor((N - 1) / 7) + 2,
	Col is (N - 1) rem 7,
	board(B,Row,Col,day(N)).

Pieces

Let's number the pieces as follows:

Define each piece and possible orientations:

%%% New representation piece/5
%%% piece(NUM,X,MaxX,MaxY,List) anchors at (X,Y) top-left
%%% 46 shape configurations
%%% each sublist shares same Y, Y+1, Y+2 etc.

%%% MaxX, MaxY savings: M1 Max  694.612 CPU vs. 1104.669 CPU
%%%              Intel Core i9 2289.239 CPU

%%% full rectangle
%%% 1 2 3	XXX
%%% 4 5 6	XXX
piece(1,X,4,5,
      [[[X,X+1,X+2],[X,X+1,X+2]] % 3 x 2
      ]).
%%% full rectangle
%%% 1 2		XX
%%% 3 4		XX
%%% 5 6		XX
piece(1,X,5,4,
      [[[X,X+1],[X,X+1],[X,X+1]] % 2 x 3
      ]).

%%% rectangle missing a corner (4 orientations)
%%% 1 2 3 	XXX XX  XXX  XX
%%% 4 5		XX  XXX  XX XXX
piece(2,X,4,5,
      [[[X,X+1,X+2],[X,X+1]],	% 3 x 2 (-6)
       [[X,X+1],[X,X+1,X+2]],	% 3 x 2 (-3)
       [[X,X+1,X+2],[X+1,X+2]], % 3 x 2 (-4)
       [[X+1,X+2],[X,X+1,X+2]] % 3 x 2 (-1)
      ]).
%%% rectangle missing a corner (4 orientations)
%%% 1 2 	X   X XX XX
%%% 3 4		XX XX XX XX
%%% 5		XX XX  X X
piece(2,X,5,4,
      [[[X],[X,X+1],[X,X+1]],	% 2 x 3 (-2)
       [[X+1],[X,X+1],[X,X+1]],	% 2 x 3 (-1)
       [[X,X+1],[X,X+1],[X+1]],	% 2 x 3 (-5)
       [[X,X+1],[X,X+1],[X]]	% 2 x 3 (-6)
      ]).

%%% U (2 orientations)
%%% 1 2 3 	X X XXX
%%% 4 5 6	XXX X X
piece(3,X,4,5,
       [[[X,X+2],[X,X+1,X+2]],	% 3 x 2 (-2)
	[[X,X+1,X+2],[X,X+2]]	% 3 x 2 (-5)
      ]).
%%% U (2 orientations)
%%% 1 2 	XX XX
%%% 3 4		 X X
%%% 5 6		XX XX
piece(3,X,5,4,
       [[[X,X+1],[X+1],[X,X+1]], % 2 x 3 (-3)
       [[X,X+1],[X],[X,X+1]]	 % 2 x 3 (-4)
       ]).

%%% L (4 orientations)
%%% 1 2 3 4 	XXXX X    XXXX    X
%%% 5 6 7 8	X    XXXX    X XXXX
piece(4,X,3,5,
      [[[X,X+1,X+2,X+3],[X]],	% 4 x 2 (+5)
       [[X],[X,X+1,X+2,X+3]],	% 4 x 2 (+1)
       [[X,X+1,X+2,X+3],[X+3]],	% 4 x 2 (+8)
       [[X+3],[X,X+1,X+2,X+3]]	% 4 x 2 (+4)
      ]).
%%% L (4 orientations)
%%% 1 2 	XX XX X   X
%%% 3 4		X   X X   X
%%% 5 6		X   X X   X
%%% 7 8		X   X XX XX
piece(4,X,5,3,
      [[[X,X+1],[X],[X],[X]],	% 2 x 4 (+2)
       [[X,X+1],[X+1],[X+1],[X+1]], % 2 x 4 (+1)
       [[X],[X],[X],[X,X+1]],	    % 2 x 4 (+8)
       [[X+1],[X+1],[X+1],[X,X+1]]  % 2 x 4 (+7)
      ]).

%%% T asymmetric (4 orientations)
%%% 1 2 3 4 	XXXX XXXX  X     X
%%% 5 6 7 8	 X     X  XXXX XXXX
piece(5,X,3,5,
      [[[X,X+1,X+2,X+3],[X+1]],	% 2 x 4 (+6)
       [[X,X+1,X+2,X+3],[X+2]],	% 2 x 4 (+7)
       [[X+1],[X,X+1,X+2,X+3]], % 2 x 4 (+2)
       [[X+2],[X,X+1,X+2,X+3]]	% 2 x 4 (+3)
      ]).
%%% T asymmetric (4 orientations)
%%% 1 2 	X  X   X  X
%%% 3 4 	XX X  XX  X
%%% 5 6		X  XX  X XX
%%% 7 8		X  X   X  X
piece(5,X,5,3,
      [[[X],[X,X+1],[X],[X]],	% 4 x 2 (+4)
      [[X],[X],[X,X+1],[X]],	% 4 x 2 (+6)
       [[X+1],[X,X+1],[X+1],[X+1]], % 4 x 2 (+3)
       [[X+1],[X+1],[X,X+1],[X+1]]  % 4 x 2 (+5)
      ]).

%%% L symmetric (4 orientations)
%%% 1 2 3 	XXX XXX   X X
%%% 4 5 6	X     X   X X
%%% 7 8 9	X     X XXX XXX
piece(6,X,4,4,
      [[[X,X+1,X+2],[X],[X]],	% 3 x 3 (top-left)
       [[X,X+1,X+2],[X+2],[X+2]], % 3 x 3 (top-right)
       [[X+2],[X+2],[X,X+1,X+2]], % 3 x 3 (bottom-right)
       [[X],[X],[X,X+1,X+2]]	  % 3 x 3 (bottom-left)
      ]).

%%% Z 
%%% 1 2 3	XX  X     X  XX
%%% 4 5 6	 X  XXX XXX  X
%%% 7 8 9	 XX   X X   XX 
piece(7,X,4,4,
      [[[X,X+1],[X+1],[X+1,X+2]], % 3 x 3 Z
       [[X],[X,X+1,X+2],[X+2]],	  % 3 x 3 Z 90
       [[X+2],[X,X+1,X+2],[X]],	  % 3 x 3 Z -90
       [[X+1,X+2],[X+1],[X,X+1]]  % 3 x 3 Z backwards
      ]).

%%% long Z asymmetric (4 orientations)	
%%% 1 2 3 4	  XX XX   XXX   XXX
%%% 5 6 7 8	XXX   XXX   XX XX
piece(8,X,3,5,
      [[[X+2,X+3],[X,X+1,X+2]], % Z backwards
       [[X,X+1],[X+1,X+2,X+3]],	% Z
       [[X,X+1,X+2],[X+2,X+3]],	% Z backwards mirror(v)
       [[X+1,X+2,X+3],[X,X+1]]	% Z  mirror(v)
      ]).
%%% long Z asymmetric (4 orientations)
%%% 1 2 	X   X  X X
%%% 3 4		XX XX  X X
%%% 5 6		 X X  XX XX
%%% 7 8		 X X  X   X
piece(8,X,5,3,
      [[[X],[X,X+1],[X+1],[X+1]], % Z 90
       [[X+1],[X,X+1],[X],[X]],	  % Z 90 mirror(v)
       [[X+1],[X+1],[X,X+1],[X]], % Z -90
       [[X],[X],[X,X+1],[X+1]] % Z -90 mirror(v)
      ]).

Piece Placement

Basic method is to place one piece at a time from piece 1 through piece 8:

%% place list of pieces on board B
placeL([],_).
placeL([P|Ps],B) :- place1(P,B), placeL(Ps,B).

%% place piece P on B at (X,Y) valued V
place1(P,B) :- enum(B,X,Y,V), place(P,V,X,Y,B).

%% place piece P with selected orientation O at (X,Y) onto board B
%% HACK: top-left (V) occupied, select shapes with empty top-left only
%% if already occupied, fails and re-selects
place(P,V,X,Y,B) :-
	(var(V) ->  select(P,X,Y,O) ; select_e(P,X,Y,O)),
	all_sqs(O,Y,B,P).

%% piece N select an orientation O anchored at (X,Y)
%% (X,Y) given, check against Mx, My for efficiency
select(N,X,Y,O) :- piece(N,X,Mx,My,Os), X =< Mx, Y =< My, member(O,Os).

%% Positions: 
%% [[X coords],[X coords]...]
%%  row Y      row Y+1
%%  all_sqs(Positions, Y, Board, P)
all_sqs([],_,_,_).
all_sqs([R|Rs],Y,B,P) :-
	nth(Y,B,Row),
	sqs_row(R,Row,P),
	Y1 is Y+1,
	all_sqs(Rs,Y1,B,P).

%% X-coord squares on selected Row (Yth)
sqs_row([],_,_).
sqs_row([X|Xs],Row,P) :-
	Xp is eval(X), nth(Xp,Row,P), sqs_row(Xs,Row,P).
	
%% N num: select
nth(N,[X|L],P) :- N == 0 -> P = X ; M is N-1, nth(M,L,P).

Notes:

select_e/4 is just an optimization, i.e. special case, of select/4 for which location (X,Y) is empty for the selected piece.
This is conceptually unnecessary, but reduces search in practice.
Therefore, piece_e/5 is just piece/5 optimized for select_e/4 (instead of select/4).
piece_e/5 is the subset of piece/5 such that the top-left corner at (X,Y) is empty.
Reduction of search obtains since there are only 15 possibilities for piece_e/5 instead of the full 46 for piece/5.
all_sqs/4 fills the board locations with the piece number P.

Given a board, enum/4, generates (X,Y) with value V at that location for possible X and Y, as long as V is not 0 (off-board).

%% enumerate X and Y, report value V of piece
%% HACK: fail when piece valued 0 (end of row, see initial board above)
% top-left cannot work,overlaps with MaxX MaxY
%%% here rules out slightly earlier
enum(B,X,Y,V) :- nth(B,0,Y,Row), nth(Row,0,X,V), V \== 0.

%% select Nth item X from list (enumerate)
%% call with N = 0 initially
nth([X|_],N,N,X).
nth([_|L],N,M,X) :- N1 is N+1, nth(L,N1,M,X).

Piece_e

A subset of piece/5 for which the top-left corner (X,Y) is empty.

%% piece_e(P,X,MaxX,MaxY,List) empty top-left only
%% Optimization for speed
%% 15 shapes configurations only, cf. 46 configurations piece/5 
%% P = 1 and 3 omitted, top-left always filled
piece_e(2,X,4,5,
	[[[X+1,X+2],[X,X+1,X+2]] % 3 x 2 (-1)
	]).
piece_e(2,X,5,4,
	[[[X+1],[X,X+1],[X,X+1]] % 2 x 3 (-1)
	]).
piece_e(4,X,3,5,
	[[[X+3],[X,X+1,X+2,X+3]] % 4 x 2 (+4)
	]).
piece_e(4,X,5,3,
	[[[X+1],[X+1],[X+1],[X,X+1]] % 2 x 4 (+7)
	]).
piece_e(5,X,3,5,
	[[[X+1],[X,X+1,X+2,X+3]], % 2 x 4 (+2)
	 [[X+2],[X,X+1,X+2,X+3]]  % 2 x 4 (+3)
	]).
piece_e(5,X,5,3,
	[[[X+1],[X,X+1],[X+1],[X+1]], % 4 x 2 (+3)
	 [[X+1],[X+1],[X,X+1],[X+1]]  % 4 x 2 (+5)
	]).
piece_e(6,X,4,4,
	[[[X+2],[X+2],[X,X+1,X+2]] % 3 x 3 (bottom-right)
	]).
piece_e(7,X,4,4,
	[[[X+2],[X,X+1,X+2],[X]], % 3 x 3 Z -90
	 [[X+1,X+2],[X+1],[X,X+1]] % 3 x 3 Z backwards
	]).
piece_e(8,X,3,5,
	[[[X+2,X+3],[X,X+1,X+2]], % Z backwards
	 [[X+1,X+2,X+3],[X,X+1]]  % Z  mirror(v)
	]).
piece_e(8,X,5,3,
	[[[X+1],[X,X+1],[X],[X]],  % Z 90 mirror(v)
	 [[X+1],[X+1],[X,X+1],[X]] % Z -90
	]).

Board Printing

All solutions for September 6th:

Assume solutions have been recorded in the database as facts soln/1.

prBoards(_) :-
	nb_setval(count,0),
	soln(B),
	nb_getval(count,N),
	M is N+1,
	nb_setval(count,M),
	prBoard(B),
	fail.
prBoards(N) :- nb_getval(count,N).

prBoard([]) :- nl.
prBoard([R|Rs]) :- prRow(R), prBoard(Rs).

prRow([]) :- nl.
prRow([X|L]) :- prCell(X), prRow(L).

prCell(X) :-
	(var(X) -> write('  ')
	; (X == 0 -> ansi_format([fg('#EBDBDB')],'␣␣',[])
	  ; (X = day(N) -> (N > 9 -> format('~d',[N]) ; format(' ~d',[N]))
	    ; (atom(X) -> write(X)
	      ; color(X,C),
	        ansi_format([fg(C)],'██',[]))))).

color(1,black).
color(2,'#818383').
color(3,red).
color(4,green).
color(5,yellow).
color(6,blue).
color(7,magenta).
color(8,cyan).

Download source: calendar.prolog.zip.

Last modified: Tue Nov 21 18:54:20 MST 2023